TÉCNICAS DE LAS VARIABLES ARTIFICIALES
Exsiten problemas de programación lineal que no proporcionan una solución básica inicial. Esta situación se presenta cuando al menos una de las restricciones es del tipo (<=) o (=). Para este propósito se desarrollan 2 métodos basados en el uso de variables artificiales: El método M o de penalización y la técnica de 2 fases.
METODO M O DE PENALIZACIÓN.
Los pasos básicos del método M son los siguientes:
1. Exprese el problema en forma estándar transformando las inecuaciones en ecuaciones introduciendo variables de holgura.
2. Agregue variables no negativas al lado izquierdo de cada una de las ecuaciones correspondientes a las restricciones de tipo (>=) o (=). Estas variables se denominan variables artificiales y su adición hace que las restricciones correspondientes.
Esta dificultad se elimina asegurando que las variables sean 0 en la solución final. Esto se logra asignando una penalización muy grande por unidad a estas variables en la función objetivo. Tal penalización se designará como –M para problemas de maximización y +M para problemas de minimización.
3. Utiliza las variables artificiales en la solución básica inicial; sin embargo la función objetivo de la tabla inicial se prepara adecuadamente para expresarse en términos de las variables no básicas únicamente. Esto significa que los coeficientes de las variables artificiales en la función objetivo deben ser 0 un resultado que puede lograrse sumando múltiplos adecuados de las ecuaciones de restricción al renglón objetivo.
4. Proceda con los pasos regulares del método simplex.
EJEMPLO:
Minimizar ![]()
Sujeto a:
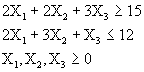
Minimizar ![]()
Sujeto a:
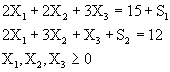
Minimizar ![]()
Sujeto a:
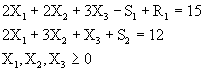
![]()
Minimizar ![]()
Sujeto a:
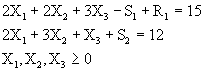

|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
R1 |
Solución |
|
Z |
1 |
-3 |
-2 |
-4 |
0 |
0 |
-M |
0 |
|
R1 |
0 |
2 |
2 |
3 |
-1 |
0 |
1 |
15 |
|
S2 |
0 |
2 |
3 |
1 |
0 |
1 |
0 |
12 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
R1 |
Solución |
|
Z |
1 |
-3+2M |
-2+2M |
-4+3M |
-M |
0 |
0 |
15M |
|
R1 |
0 |
2 |
2 |
3 |
-1 |
0 |
1 |
15 |
|
S2 |
0 |
2 |
3 |
1 |
0 |
1 |
0 |
12 |
Criterio para seleccionar la variable entrante:
Maximización : El valor mayor negativo del renglón Z.
Minimización : El valor mayor positivo del renglón Z.
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
R1 |
Solución |
|
Z |
1 |
-1/3 |
2/3 |
0 |
-4/3 |
0 |
4/3-M |
20 |
|
X3 |
0 |
2/3 |
2/3 |
1 |
-1/3 |
0 |
1/3 |
5 |
|
S2 |
0 |
4/3 |
7/3 |
0 |
1/3 |
1 |
-1/3 |
7 |
|
V.B. |
Z |
X1 |
X2 |
X3 |
S1 |
S2 |
R1 |
Solución |
|
Z |
1 |
-5/7 |
0 |
0 |
-10/7 |
-2/7 |
10/7-M |
18 |
|
X3 |
0 |
2/7 |
0 |
1 |
-3/7 |
-2/7 |
3/7 |
3 |
|
X2 |
0 |
4/7 |
1 |
0 |
1/7 |
3/7 |
-1/7 |
3 |
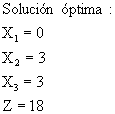
EJEMPLO:
Maximizar ![]()
Sujeto a:
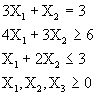
Maximizar ![]()
Sujeto a:
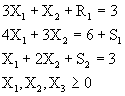
Maximizar ![]()
Sujeto a:
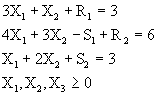
Maximizar ![]()
Sujeto a:
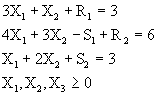
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
-4 |
-1 |
0 |
0 |
M |
M |
0 |
|
R1 |
0 |
3 |
1 |
0 |
0 |
0 |
0 |
3 |
|
R2 |
0 |
4 |
3 |
-1 |
0 |
1 |
1 |
6 |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
3 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
-4-7M |
-1-4M |
M |
0 |
0 |
0 |
-9M |
|
R1 |
0 |
3 |
1 |
0 |
0 |
0 |
0 |
3 |
|
R2 |
0 |
4 |
3 |
-1 |
0 |
1 |
1 |
6 |
|
S2 |
0 |
1 |
2 |
0 |
1 |
0 |
0 |
3 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
1/3-5/3M |
M |
0 |
4/3+7/3M |
0 |
4-2M |
|
X1 |
0 |
1 |
1/3 |
0 |
0 |
1/3 |
0 |
1 |
|
R2 |
0 |
0 |
5/3 |
-1 |
0 |
-4/3 |
0 |
2 |
|
S2 |
0 |
0 |
5/3 |
0 |
1 |
-1/3 |
1 |
2 |
|
V.B. |
Z |
X1 |
X2 |
S1 |
S2 |
R1 |
R2 |
Solución |
|
Z |
1 |
0 |
0 |
1/5 |
0 |
8/5+M |
-1/5+M |
18/5 |
|
X1 |
0 |
1 |
0 |
1/5 |
0 |
3/5 |
3/5 |
|
|
R2 |
0 |
0 |
1 |
-3/5 |
0 |
-4/5 |
3/5 |
6/5 |
|
S2 |
0 |
0 |
0 |
1 |
1 |
1 |
-1 |
1 |